Bezier Curve and B-Spline Curve: Many types of curves can be used for numerical analysis, mathematics and computer graphics applications. Two popular curve models in such areas of analysis are Bezier Curves and B-Spline Curves; experts sometimes consider B-Spline an alternative form of Bezier. There are similarities between the two curves while there are also numerous distinctions which will be addressed herein.
What Is Bezier Curve?
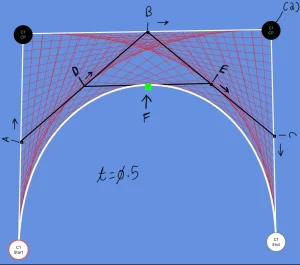
Bezier curves, which are parametric curves, are used across many fields to model smooth surfaces. Their features include being infinitely scalable, being modified easily and intuitive. Bezier curves have also become popular tools used by animators when discussing motion in animated videos – these Bezier curves being often referenced when discussing physics behind these animations. Paul de Castlejau developed these curves using Castlejau’s algorithm; French designer Pierre Bezier first made them popular by using them while modeling automobiles using them to design vehicles back in 1962.
Bezier curves of higher degrees can be challenging to draw or evaluate, so here is an example of a Bezier equation involving two points.
B(t) = P0 + t(P1- P0) = (1 – t)P0+tP1, te[0,1].
What Is a B-Spline Curve?
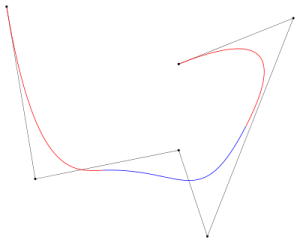
B-Spline curves are generalizations of Bezier Curves that share many similar properties; however, B-Spline Curves offer more desirable properties than their Bezier counterparts and require more information for curvatures such as degree of bend and knot vector; they also possess more complicated theories.
However, they offer many advantages which help offset this shortcoming. A B-Spline curve can easily be converted to a Bezier Curve when desired by its creator and offers greater flexibility and control than Bezier curves; lower degree curves are supported while more control points can be maintained than with Beziers. Polynomials such as B Spline curves don’t represent simple shapes such as circles or ellipses effectively but NURBS provides generalized versions that can create these forms more readily.
Importance of Bezier Curve and B-Spline Curve in design and animation
Curves are essential components in both design and animation, offering numerous applications and benefits for use across a wide array of projects. In animation specifically, curves play an integral part of this field for many reasons.
- Smoothness and Aesthetics: Curves create visually pleasing shapes and transitions that are aesthetically pleasing to the human eye. Designers and animators can utilize curves to achieve natural, organic-looking forms with pleasing animations or designs using them.
- Shape Control: Curves offer designers precise control of an object’s form. By manipulating control parameters and curve parameters, designers can change contours of designs as desired – especially useful when creating intricate or complex shapes.
- Flexible and Versatile: Curves are extremely versatile tools, used to form various shapes and structures. Curves can be used to model simple and complex objects ranging from geometric to organic forms – perfect for design and animation applications alike.
- Animation and Motion Paths: Curves provide animators with an effective means of creating animation motion paths. By animating objects along curves, animators can produce realistic motions for character animations, camera movements and objects moving within scenes. Curves provide precise control of both timing and trajectory when animating elements in a scene.
- Interpolation and Blending: Curves provide seamless interpolation or blending of keyframes and control points, which is essential for smooth animations and transitions between states or poses. Designers can create realistic transitions by creating curves between control points.
- Parametric Modeling: Curves play an essential part in parametric modeling. Their use can produce complex surfaces and shapes that can easily be modified through changing parameters or control points – providing iterative design processes with more efficiency while exploring various design possibilities.
- Visual Effects: Curves play an important role in creating visual effects such as fluid simulations and particle systems, with designers and animators being able to use curves as tools to define behavior and motion for visually striking results.
Curves are key elements in animation and design, offering control, flexibility, and smoothness for animating realistic animations and creating captivating visual effects. Curves play an essential part in producing appealing designs that offer control, flexibility, and smoothness that engage viewers and viewers alike.
Bezier Curves:
Bezier curves can be found in many computer graphics applications, from design and animation to architecture and engineering. Introduced by French engineer Pierre Bezier in the 1960s while working for a Renault car manufacturer, these curves have a series of control points that determine their behavior and shape.
- Mathematically, a Bezier curve with degree n can be described using its control points and equation. These anchor points determine both its curvature and trajectory – starting with one control and ending at another while intermediate control points shape its form in between.
- Interpolation and blending techniques can be used to form Bezier Curves. De Casteljau’s algorithm and Bernstein polynomials are two popular ways of calculating points along a Bezier curvature.
- De Casteljau’s algorithm is an iterative process that breaks up a curvature into smaller segments and then computes points based on weighted averaging of control points, creating a smoother and more precise rendering of curves. If more points are desired for smoothness or precision then repeat subdividing can occur, leading to smoother rendering results.
- Bernstein polynomials provide another means of calculating points on a bezier curvature. Each control point contains its own Bernstein Polynomial; the curve can then be determined by multiplying all these polynomials together.
Bezier curves possess several properties and characteristics that make them useful in computer graphics:
- Control Points and Polygon: Arranging and positioning control points is what determines the shape of any curvature. Connected points form a polygon control that visually represents this curve shape.
- Degree and Order: Bezier Curves have degrees that are one less than their number of control points; thus their Order equals this value. Higher degrees can produce more complex curves while providing increased control.
- Convex Hull Property: Bezier curves always fall within the convex hull defined by their control points, providing predictable and controlled shapes.
Bezier curves offer many advantages, including smoothness, control of shape, and ease of representation. Beziers can be created and adjusted in such a way as to give precise control of their shape – though beziers tend to be less flexible than other forms as their shape requires adjustment of control points in order to be altered.
Bezier curves can be found across many fields of computer-aided design (CAD), animation, font design, and computer graphics. Beziers are commonly employed to create smooth paths or model and animate objects or define character poses and movements – they’re even often part of digital design workflows thanks to their ease and intuitive nature.
B-Spline Curves:
B-spline curvatures are another type of shape used extensively in animation, computer graphics, and design. Their namesake is “B-spline,” or “basis curve,” referring to the mathematical functions that define their curves. B-spline curvatures first appeared as a generalization to Bezier curves back in 1960.
- B-splines are defined by control points and knot vectors, with each knot serving to determine how each control point affects the curve. A B-spline with degree n can be mathematically defined using n+1 control points knotted with n+m+2 knots.
- Each control is associated with its own set of basis functions that determine the shape of a B-spline, often piecewise polynomial functions representing interpolation or influence between adjacent control points.
- Local control is one of the hallmarks of B-spline curves, in contrast to bezier curves where changing one point of control impacts an entire curve, this feature of B spline curvatures provides more precise control and flexibility over how your curvature shapes out.
- B-spline curves offer greater continuity than bezier curves, enabling designers to adjust the knot vector to achieve different smoothness levels for smooth transitions between curve segments – such as C0 (positional continuity), C1(tangent continuity), or C2(curvature continuation). B-spline curvatures make an excellent solution for seamless transitions between curve segments, providing designers with greater control of smoothness and continuity than with bezier curves.
The B-spline offers numerous advantages and characteristics:
- Control Points and Control Polygon: B-spline Curves also use control polygons to define their curves. Their shape is determined by an arrangement and placement of control points which, combined with line segments connecting these points, form a polygon control that visually represents its form.
- Degree and Order: A curve’s degree is determined by taking its maximum power among the basis functions that were used to define it; B spline orders equal the degree plus one. As its degree increases, more complex yet controllable shapes may result from it.
- Local Control and Continuity: B-spline curvatures provide localized control and continuity by permitting modifications to only certain portions of a curve, while offering different degrees of continuity for seamless transitions and connections between curve segments.
B-spline curvatures can be applied across several fields including computer graphics, animation and shape modeling. Their applications range from creating smooth and continuous paths for animation purposes to designing curves with precise control over shape and continuity.
B-spline curvatures offer greater flexibility, local control, and higher levels of consistency when compared to beziers, although they may be mathematically more complex due to requiring basis functions to be calculated.
Advantages of Bezier Curve
Advantages Bezier curves have long been used in computer graphics, animation, and design due to their many benefits. Bezier curves offer several key advantages which are widely recognized across these fields.
- Smoothness and Shape Control: Bezier curves create elegant, visually appealing shapes, allowing designers to alter its curvature by manipulating its control point. Beziers allow designers to easily produce simple or complex curvatures while still achieving smoothness and beauty in design projects.
- Bezier Curves offer an intuitive and straightforward representation: Their mathematical formula is straightforward, as are their control points which have direct control over their shape – making Beziers easy to manipulate and understand in design workflows, and rapid iteration processes.
- Convex Hull Property: Bezier curves always lie within the convex hull defined by their control points, providing predictable and controlled shapes that eliminate self-intersections and abrupt changes to their behavior.
- Efficient Rendering and Evaluation: Bezier curves can be rendered and evaluated efficiently using algorithms such as De Casteljau’s algorithm for quick calculation of points along their paths, enabling real-time rendering and interactive manipulation – an efficiency which makes these curves ideal for applications, interactive design tools, or similar software solutions.
- Shape Interpolation: Bezier curves provide smooth interpolation between control points. Designers can create animations and transitions by setting keyframes or control points and smoothly interpolating different shapes. This technique can be used for character animations, shape morphing, or transitions between poses or states seamlessly.
- Well-Supported in Software and Tools: Bezier curves are widely supported by various software applications and tools, from graphic editing software, modeling applications, and animation tools all the way through to graphic designing programs and design applications. As such, Beziers make life simpler for designers using multiple platforms by being easier for them to utilize them efficiently.
- Scalability and Efficiency: Bezier curves can easily be scaled, rotated, and translated without altering their original form. Scalability makes adjusting and transforming curves for different situations like resizing objects or repositioning them easier; beziers also offer versatility that’s great for animation and design projects as they can be quickly and efficiently adjusted and transformed by design professionals.
Bezier curves are an invaluable design and animation tool, offering smoothness, shape control, and simplicity. Accessible both to beginners as well as experts due to their intuitive software representation and support, bezier curves can make animation simple yet strikingly realistic.
Disadvantages of Bezier Curve
Bezier curves have many advantages, but there are also some restrictions and drawbacks that should be considered when using them. Bezier curves do have their share of disadvantages to take into account.
- Limited Flexibility: Bezier curves are less flexible than other forms of curves such as B-spline. To alter its shape, you may have to alter its control points; creating complex or irregular shapes may require fine control over how its behavior develops.
- Lack of Local Control: Adjusting any one of the control points within a Bezier Curve will have an immediate and dramatic impact on its shape, yet modifying control points does not offer localized controls; consequently it may be challenging to fine-tune specific areas or details within it due to this.
- Curve Editing Is Difficult: Editing Bezier Curves can be complex. Modifying them requires manipulation of control points that may lead to unwanted or unexpected changes in behavior; further adjustments and control point manipulation will likely be necessary in the iterative adjustment process.
- Limited Continuity: Bezier curves have an inherent limit in terms of continuity. Though position continuity (C0) at the control point can be reached, reaching higher continuity levels such as tangent continuity (C1) or curvature continuity (C2) may require additional techniques or interpolations methods – possibly impacting visual continuity and smoothness of the curve.
- Difficulty in Interpolation: Interpolating between control points on a Bezier Curve may not always result in precise results due to their mathematical nature; interpolating points between control points may produce deviations and inaccuracies that erode accuracy over time.
- Complexity with Higher Degrees: Bezier curves of higher degrees are both mathematically and computationally complex, requiring more control points that make it more challenging to manipulate and manage them, as well as taking more resources to compute.
Bezier curves remain popularly used in design and animation despite their drawbacks, providing an ideal blend of simplicity, smoothness, control and controllability for many applications. In more complex or flexible scenarios that require local control or greater continuity than beziers might provide the better solution; B-spline curvatures may offer greater continuity than these options.
Advantages of B-Spline Curve
B-spline curvatures offer many benefits that make them an excellent choice for computer graphics, animation, and design. Here are the main ones.
- Localized Control: The B-spline provides localized control, meaning that changing a control point only affects small sections of a curve, giving designers greater flexibility when shaping and refining curvatures.
- Higher Continuity: B-spline Curves Provide Increased Continuity When Contrasted to Bezier Curves. Designers can adjust the knot vector for different levels of continuity and smoothness – for instance, C0 (position consistency), C1(tangent continuity), and C2(curvature continuation). Thus B-spline curvatures make for effortless transitions.
- Flexibility in Editing: B-spline Curves allow designers more freedom when editing or modifying than bezier Curves. By simply changing a control point, designers can more intuitively and predictably adjust a B-spline Curve without disrupting its overall shape. They allow for smooth refinements as well as add or delete control points without disturbing its overall form.
- Versatility in Shape Representation: B-spline Curves offer more flexible shape representation than Bezier curves, representing various shapes with fewer control points compared to Bezier curvatures. Basis functions, knot vectors, and other tools enable efficient and compact display of complex surfaces and curves using B-spline curvatures; making this powerful tool applicable in modeling both simple and complex surfaces and curves.
- Smoothness and Interpolation: B-spline curvatures provide smooth interpolation of control points, enabling designers to craft visually pleasing curves using localized control and consistency properties of B-splines. Furthermore, their accurate interpolation points within the convex shell of control points allows precise shape representation by these curves.
- B-spline Curves Can Be Quickly Calculated and Evaluated: B-spline curvatures can be quickly computed and evaluated with algorithms like de Boor’s algorithm, which allow fast computation of curve points allowing interactive manipulation and real-time rendering. This efficiency is especially valuable in applications that require interactive and responsive curve editing.
- Smoothness and Interpolation: B-spline curvatures are supported by many design and animation tools, from graphic editing software to 3D modeling and animation packages – meaning designers and animators are able to utilize B-spline curvatures in their preferred software environment.
B-spline curvatures provide numerous advantages, including local control, greater continuity, flexibility when editing, versatility with shape representation and efficient computation. B-spline curves are an invaluable way to create and manipulate curves for various design and animation projects.
Disadvantages of B-Spline Curve
B-spline curvatures offer many advantages but also have drawbacks and limitations that limit their usage. Unfortunately, however, B-spline curves also pose various disadvantages that should be considered before choosing them as your solution.
- Increased Complexity: B-spline curvatures can be more mathematically complex than bezier curves and therefore more challenging to work with and understand due to the knot vector and needing to calculate base functions.
- Lack of intuitive Control Points: B-spline curves do not directly correspond with control points; unlike bezier curves where control points directly influence the curve’s shape, B-spline curvatures have more indirect relationships due to involvement by basis functions and knot vectors. As a result, using this method makes controlling and manipulating its shape challenging.
- B-spline Curves Provide Less Local Shape Control: Although B-spline curves provide more local control than bezier curves, their control points can be spread out over a larger area limiting localized changes to their shape. A B-spline’s control point may have an impactful ripple effect and this could impede your attempts at making localized adjustments to its form.
- Difficulty in Interpolation: Since B-spline curves do not directly interpolate control points like Bezier curves do, additional techniques such as adjusting knot vectors or adding new control points may be required to achieve desired interpolation behavior.
- Increased Computational Complexity: B-spline curves, particularly higher degree B-splines, can be more complicated to render or evaluate than bezier curves. Calculating points on B-spline curvatures involves the evaluation and summation of control point contributions – something which may prove computationally demanding.
- Knot Vector: Managing the knot vector requires careful thought. Adjusting it to achieve desired behavior or continuity can be challenging; managing it correctly helps ensure smooth curve behavior and eliminate artifacts that could otherwise derail development.
B-spline curvatures may have some drawbacks, yet their use and value in design and animation remain widely recognized. With sufficient knowledge and experience, these curves can be utilized to produce animations and shapes of desired dimensions.
Difference between Bezier and B-Spline Curves
Bezier and B-spline curvatures need to be assessed according to several key considerations, so we will explore some key differences between them:
Control and shape manipulation:
- Bezier Curves: Bezier curves feature intuitive control points which directly alter the shape of a curve, making manipulation and understanding easy; yet altering global changes to it may prove more complex.
- B-spline curvatures: B-spline shapes allow designers to control certain areas of a curve without changing its overall form, providing more precise control and less intuitive global changes.
Continuity and Smoothness:
- Bezier Curves: Bezier curves are distinguished by limited continuity, typically C0 continuity at control points. In order to attain higher levels of consistency, additional techniques or interpolations techniques may need to be utilized.
- B-spline curvatures: By altering the vector of the knot, B-splines can offer higher levels of continuity – including C0 and C1 continuity – providing smoother transitions between curve segments.
Flexibility and Versatility:
- Bezier Curves: Bezier curves can be used to easily create simple, smooth shapes. Scaling, rotation, and translation without altering their shape makes them suitable for graphics and animated film applications.
- B-spline curvatures: These curves offer more flexibility and versatility in their ability to be molded to form complex surfaces and curves, while B-spline Curves take advantage of localized control, greater continuity, and smooth transitions for modeling complex shapes with ease.
Interpolation and Accuracy:
- Bezier Curves: Bezier curves provide precise interpolation by interpolating between control points to create precise interpolation. Placing points along this curve may prove challenging at times.
- B-spline Curvatures: Though B-spline shapes don’t actually interpolate control points directly, they can interpolate within their convex shell for precise representation and interpolation. This results in accurate representation and interpolation.
Computational Complexity:
- Bezier Curves: Bezier curves are computationally efficient even with higher degrees.
- B-spline Curves: Due to their more complex structures and the need to calculate basis functions, B-spline shapes may require more complex mathematical and computational calculations than expected.
Bezier curves are easy to use and offer intuitive control points, making them perfect for simple shapes or global modifications. B-spline curvatures provide localized control with greater accuracy. These make for smooth transitions between complex forms.
Comparison Table:
| Bezier Curves | B-spline Curves |
|---|---|
| Intuitive control points directly influence the entire curve. | Localized control points allow for specific region adjustments. |
| Limited continuity between curve segments. | Higher levels of continuity achievable by adjusting the knot vector. |
| Global modifications are straightforward but can be challenging. | Precise control over localized modifications, less intuitive for global changes. |
| Suitable for simple shapes and easy to scale, translate, and rotate. | Versatile for complex shapes and smooth transitions. |
| Interpolates first and last control points precisely. Points between control points may not lie exactly on the curve. | Control points may not be interpolated directly, but accurate interpolation within the convex hull is possible. |
| Simple and efficient algorithms for rendering and evaluation. | More mathematically complex, potentially higher computational demands. |
Conclusion
Bezier curves and B-spline curves can be extensively employed in computer graphics as well as Computer-aided Design (CAD) applications to represent smooth curves. Bezier curves are characterized by an array of control points that directly influence the curve’s form. Contrary to this B-spline curves utilize mathematical base functions using control points with an influence locally, which makes it possible to make more flexible and smooth curve changes. B-splines can also accommodate higher-order curves and offer more accuracy and flexibility. The decision between these two is contingent on the specific needs and the complexity of the curves that are required during design.

